Основы беспроводных сетей
Аналоговые и цифровые сигналы. Модуляция
для учёта прогресса курса
Аналоговые и цифровые сигналы
При распространении сигналов в какой-либо среде, они носят непрерывный по величине и времени характер. Сигналы, непрерывные по величине напряжения и времени, называются аналоговыми (рисунок 1(а)). Основной причиной массового перехода от аналоговых сигналов к цифровым в беспроводных системах связи является развитие цифровой техники, которая оперирует численными данными, а не аналоговыми сигналами. Также, в пользу цифровых сигналов сыграли возможность восстановления в промежуточных узлах передачи и инструмент кодирования, используемый для восстановления утерянных данных и решения вопросов безопасности.
Если зафиксировать отсчёты сигнала в выделенные моменты времени, то такой сигнал будет называться дискретным, а операция по его получению из аналогового - дискретизацией (рисунок 1(б)). При дискретизации аналогового сигнала следует руководствоваться теоремой Котельникова, согласно которой частота дискретизации должна минимум в два раза превосходить высшую частоту спектра сигнала. В случае, если теорема Котельникова не будет выполнена, то часть данных, передаваемых в сигнале, будет утеряна. Так, при передаче сигнала в полосе 5,12 - 5,32 ГГц частота дискретизации должна быть не ниже 10,64 ГГц; при передаче сигнала в полосе 2,432 - 2,452 ГГц, частота дискретизации должна быть не ниже 4,904 ГГц.
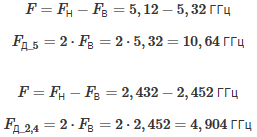
Если значения напряжения сигнала свести к нескольким конечным уровням, то полученный сигнал будет называться квантованным, а операция по его получению из аналогового - квантованием (рисунок 1(в)).
Результат двух операций, дискретизации и квантования, над аналоговым сигналом называется цифровым (рисунок 1(г)).
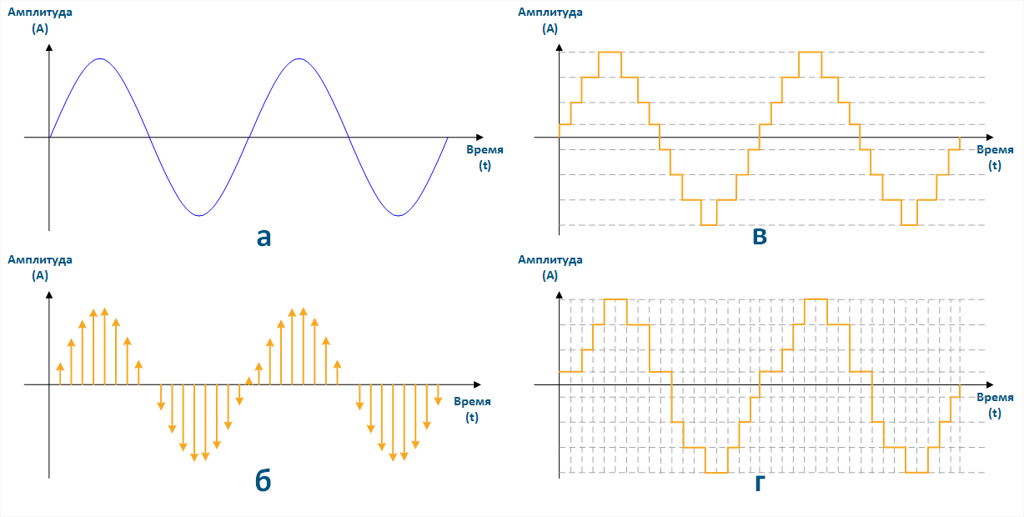
Рисунок 1 - Временные зависимости гармонического сигнала в различных представлениях: а - аналоговый, б - дискретный, в - квантованный, г - цифровой
Используя цифровые сигналы, можно представить исходный аналоговый сигнал в виде конечной числовой последовательности, что облегчит хранение и обработку данных, а также сделает возможным использование схем кодирования.
Для пояснения методики кодирования рассмотрим часть сигнала, представленного на рисунке 1(г). Для квантования сигнала используется 8 уровней, т.е. для численного обозначения каждого уровня в двоичной системе потребуется три бита. В нулевой отсчёт времени значение сигнала соответствует уровню "100", в следующий отсчёт уровень сохраняется - "100", далее значение сигнала возрастает и соответствует уровню "101", на следующем отсчёте сигнал вновь возрастает и находится на уровне "110" и т.д. Конечная запись сигнала в цифровой форме представлена на рисунке 2, т.е. исходный аналоговый сигнал представлен в виде последовательности "100100101110111111110110100100".
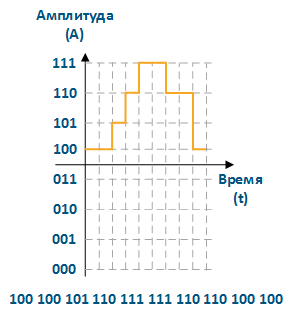
Рисунок 2 - Часть гармонического сигнала, записанного в цифровом виде
Следует иметь в виду, что при представлении аналогового сигнала в цифровой форме часть данных о сигнале будет утеряна, причём схожесть сигналов будет определяться частотой дискретизации и числом уровней квантования. По такому принципу работают музыкальные кодеки: один и тот же звуковой поток может быть закодирован различными кодеками, что влияет на размер файла записи и субъективное качество воспроизведения. Таким образом, при преобразовании аналогового сигнала в цифровой, необходимо учитывать объём выходных данных и степень важности данных, которые теряются в процессе преобразования.
Важным достоинством цифровых сигналов является возможность их воспроизведения: принятый аналоговый сигнал может быть усилен по амплитуде, однако, наряду с сигнальной составляющей, будет усилена помеха, тогда как цифровой сигнал может быть сначала декодирован, после чего сгенерирован заново.
Кодирование
Под кодированием подразумевается однозначное преобразование числовой последовательности в другую числовую последовательность, как правило, большей длины. Кодирование применяется с целью обнаружения и/или исправления ошибок, возникших при передаче данных.
Рассмотрим простейший вид кодирования с проверкой на чётность: для этого запишем числовую последовательность, полученную в предыдущем пункте, поэлементно в столбец:

Рисунок 3 - Пример кодирования числовой последовательности кодом проверки на чётность
К каждому из символов добавим дополнительный бит, который равен нулю, если сумма битов числа чётная, и равен единице, если сумма битов числа нечётная. Таким образом, сумма битов нового четырёхзначного числа является чётной.
При передаче последовательность модулирует несущий сигнал и передаётся в эфир. На приёмной стороне полученный сигнал декодируется и делится на 4-битные последовательности, каждая из которых кодирует один символ. Далее, каждое из четырёхбитных чисел проверяется на чётность и, в случае, если сумма битов является нечётной, то фиксируется ошибка в передаче данного символа. Код с проверкой на чётность может только обнаруживать одну ошибку при передаче символа, т.е. если будут неверно приняты два из четырёх битов, то ошибка обнаружена не будет. Рассмотренный метод кодирования является достаточно простым, однако существуют более сложные кодовые конструкции, которые позволяют не только обнаруживать, но и исправлять одну или несколько ошибок.
Модуляция
Сигнал, содержащий информацию, занимает определённую полосу, располагается в области низких частот и называется модулирующим. Высокочастотный сигнал, один или несколько параметров которого изменяются в соответствии с модулирующим сигналом называется модулируемым. При этом процесс преобразования высокочастотного гармонического сигнала, в ходе которого спектр информационного сигнала переносится в область высоких частот, называется модуляцией. Использование данного преобразования имеет два преимущества:
- при переносе спектра сигнала в высокочастотную область уменьшаются габариты приёмной и передающей антенн, как было показано в уроке "Антенны";
- перенос спектров сигнала на определённую частоту позволяет реализовать некоторые схемы множественного доступа, такие как FDMA, OFDMA, рассмотренные в уроке "Методы множественного доступа".
Схема модуляции
Процесс модуляции состоит в изменении амплитуды, частоты или фазы несущей частоты в соответствии с поступающими данными.
Обратимся к рисунку 4 для пояснения процесса модуляции. Генератор несущей формирует опорный сигнал, представляющий из себя гармонический сигнал заданной частоты, который поступает на вход модулятора. Источник передаваемого сообщения формирует поток бит, которые необходимо передать на приёмную сторону. В соответствии с сформированным потоком бит в блоке модулятора изменяются один или несколько параметров опорного сигнала, после чего, полученный сигнал передаётся в следующие каскады передатчика и излучается в направлении приёмника.
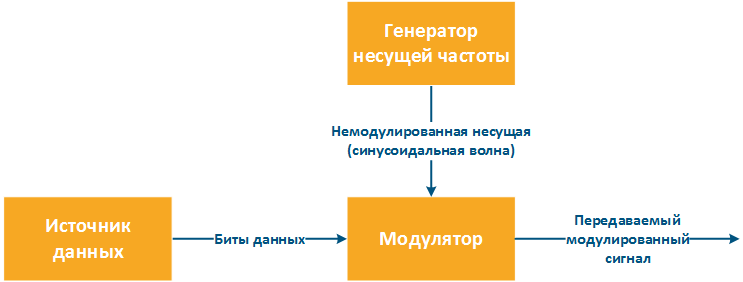
Рисунок 4 - Схема модуляции
Сигнальное созвездие IQ
Одним из инструментов при оценке схемы модуляции сигнала является изображение сигнального созвездия, которое представляет из себя способ представления радиосигнала в виде двухмерной точечной диаграммы на комплексной плоскости. Любой сигнал может быть представлен как сумма синфазной (I) и квадратурной (Q) составляющих и изображается как точка на комплексной плоскости. Совокупность сигналов, которую формирует передатчик и которая, исказившись в процессе распространения, детектируется на приёмной стороне, образует на комплексной плоскости множество точек, называемых сигнальным созвездием.
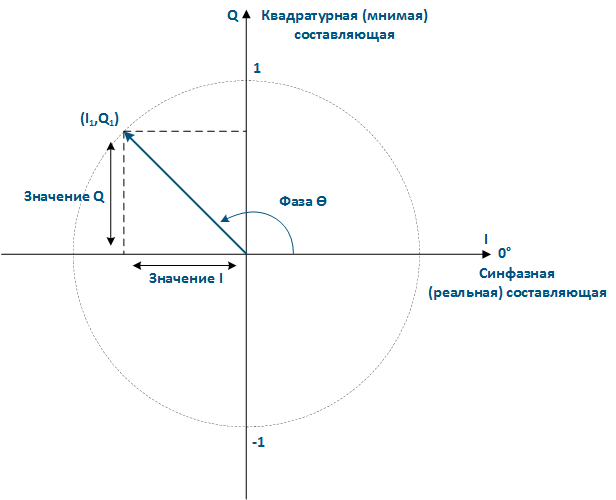
Рисунок 5 - Система координат, используемая при отображении сигнального созвездия
Для примера рассмотрим систему с двоичной фазовой манипуляцией (BPSK), которая подробнее будет рассмотрена ниже. Для передачи символа "1" используется сигнал с нулевой начальной фазой, для передачи символа "0" - сигнал, смещённый на π, относительно первого, т.е. в системе разрешены только два сигнала, а при приёме сигнала со значением фазы, отличной от разрешённых, сигнал будет соотнесён к одному из заданных. Таким образом, сигнальное созвездие для рассмотренного примера будет выглядеть следующим образом:
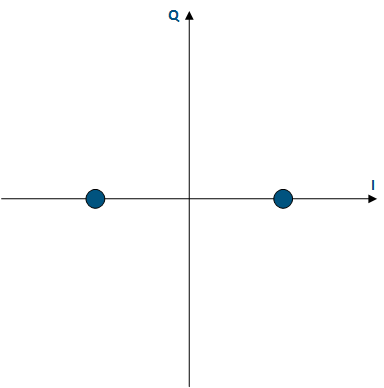
Рисунок 6 - Сигнальное созвездие для BPSK (ФМ-2)
Рассмотрим пример передачи потока данных "10110100" с использованием разных видов модуляции. В принятой терминологии различают модуляцию аналоговых и цифровых сигналов - модуляцию цифровых сигналов называют манипуляцией. Дальнейшие примеры будут рассмотрены для цифровых сигналов, поэтому будет использоваться понятие манипуляции.
Амплитудная манипуляция (ASK, AM)
При использовании амплитудной манипуляции каждому из передаваемых символов ставится в соответствие высокочастотный сигнал различной амплитуды. На рисунке 5 (б) передаваемому символу "1" ставится в соответствие сигнал с амплитудой, равной 1, а символу "0" - сигнал с амплитудой 0,5. На рисунке 5(в) используется большее число амплитуд сигнала, что позволяет передать за единичную посылку два информационных символа: символам "11" соответствует сигнал с амплитудой 1, "10" - с амплитудой 0,75, "01" - с амплитудой 0,5, "00" - с амплитудой 0,25. Таким образом, выбранная схема модуляции влияет на число информационных символов, передаваемых в рамках одной символьной посылке.
Количество уровней амплитуды сигнала зависит от аппаратных возможностей передающей и принимающей сторон, а также от характеристик канала связи и напрямую влияет на скорость передачи данных. Так, при одинаковом интервале единичной посылки, использование четырёхуровневой амплитудной манипуляции (АМ-4) повышает скорость передачи данных в два раза относительно двоичной амплитудной манипуляции (АМ-2). Данный пример показан на рисунке 7:исходная последовательность передаётся с помощью АМ-4 (рисунок 7(в)) за четыре элементарных посылки, а при использовании АМ-2 (рисунок 7(б)) - за восемь. Следует отметить, что помимо рассмотренных видов амплитудной манипуляции, возможно использование других - АМ-8, АМ-16 и т.д.
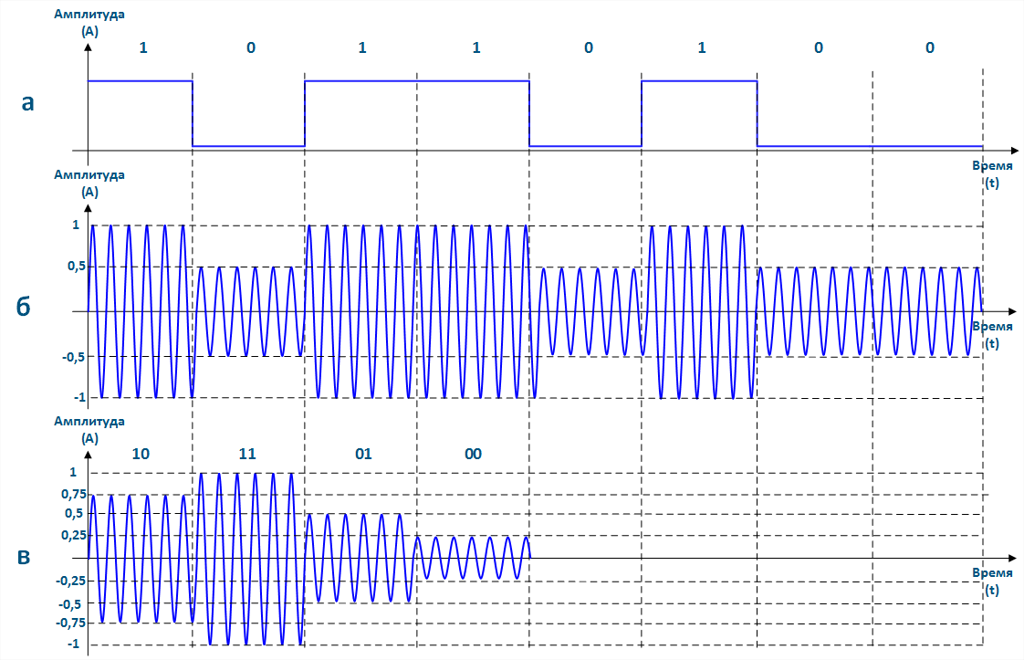
Рисунок 7 - Осциллограммы амплитудной манипуляции: а - исходная последовательность данных, б - АМ-2, в - АМ-4
Частотная манипуляция (FSK, ЧМ)
При использовании частотной манипуляции каждому из информационных символов ставится в соответствие высокочастотный сигнал определённой частоты. Так, при двоичной частотной манипуляции ЧМ-2 используется сигналы двух частот, а при ЧМ-4 - сигналы четырёх частот. Аналогично амплитудной манипуляции, число используемых сигналов влияет на скорость передачи и зависит от аппаратных возможностей оборудования и качества канала связи. На рисунке 8 изображены осциллограммы сигнала, модулированного ЧМ-2:
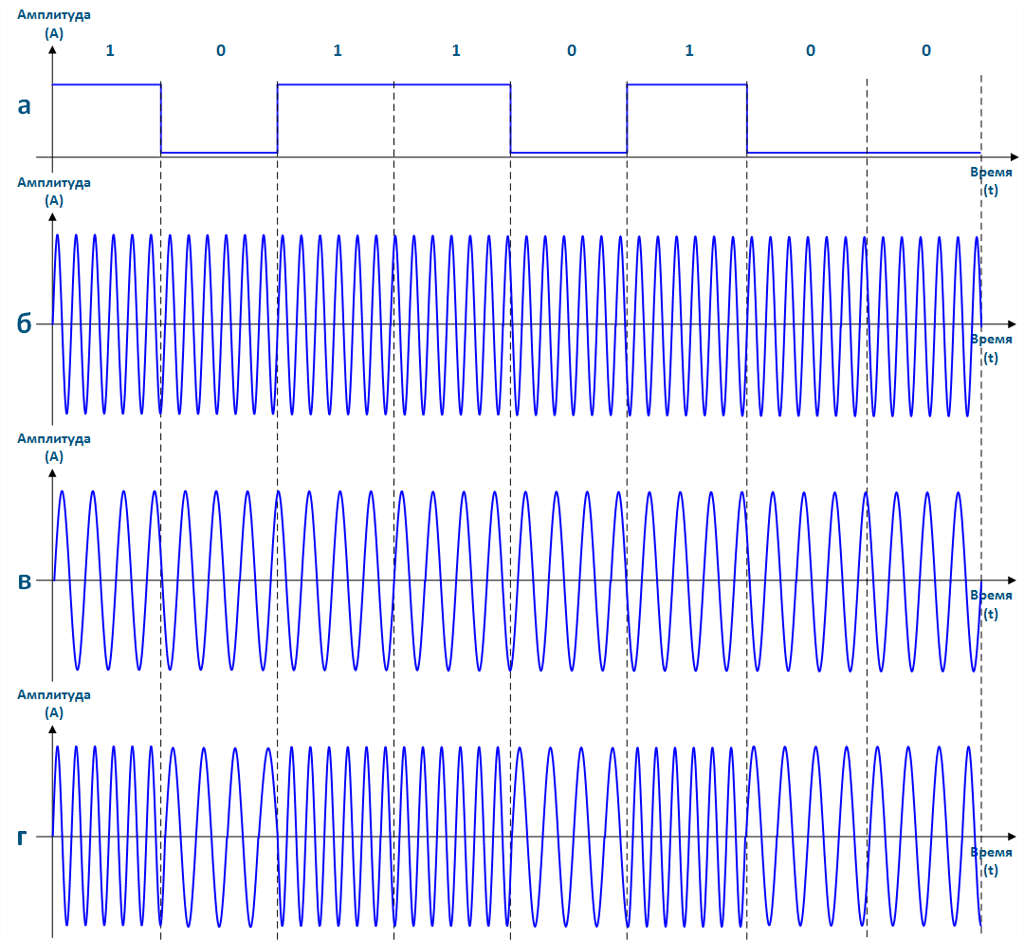
Рисунок 8 - Осциллограммы частотной манипуляции: а - исходная последовательность данных, б - сигнал, соответствующий символу "1", в - сигнал, соответствующий символу "0", г - сигнал, полученный при манипуляции ЧМ-2
Фазовая манипуляция (PSK, ФМ)
При использовании фазовой манипуляции, в соответствие передаваемым символам ставятся высокочастотные сигналы с различными значениями начальной фазы. Пример использования ФМ-2 для манипуляции последовательности данных представлен на рисунке 9: символу "1" соответствует сигнал с нулевой начальной фазой, символу "0" - сигнал со значением фазы π. Закономерности, при использовании высших степеней манипуляции ФМ-4, ФМ-8 и т.д., аналогичны амплитудной и частотной манипуляциям.
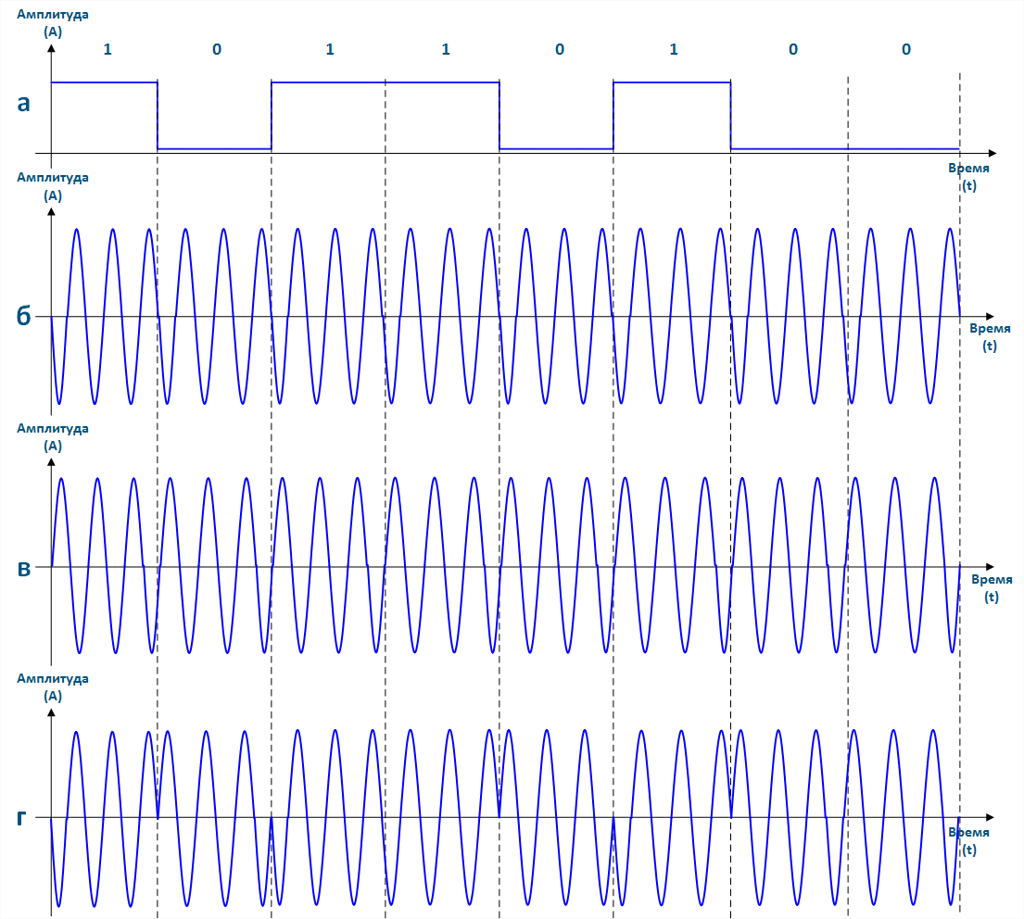
Рисунок 9 - Осциллограммы фазовой манипуляции: а - исходная последовательность данных, б - сигнал, соответствующий символу "1", в - сигнал, соответствующий символу "0", г - сигнал, полученный при манипуляции ФМ-2
Квадратурно-амплитудная манипуляция (QAM, КАМ)
В рассмотренных выше видах манипуляции, в соответствии с информационным сообщением изменялся один из параметров высокочастотного сигнала: амплитуда, частота или фаза. В квадратурно-амплитудной манипуляции используется комбинация различных амплитудных уровней и фазовых сдвигов, которые ставятся в соответствие передаваемым битам информации. Так, при использовании QAM-16 разрешено 4 значения амплитуды и 4 значения фазовых сдвигов, что при комбинации "каждый с каждым" даёт 16 возможных вариантов сигнала, каждому из которых соответствует точка на сигнальном созвездии:
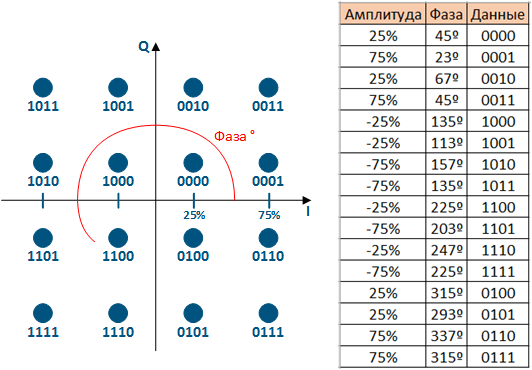
Рисунок 10 - Сигнальное созвездие QAM-16
Пусть, при передаче рассматриваемой информационной последовательности, используется QAM-16. Тогда осциллограммы модулированного сигнала будут выглядеть следующим образом:
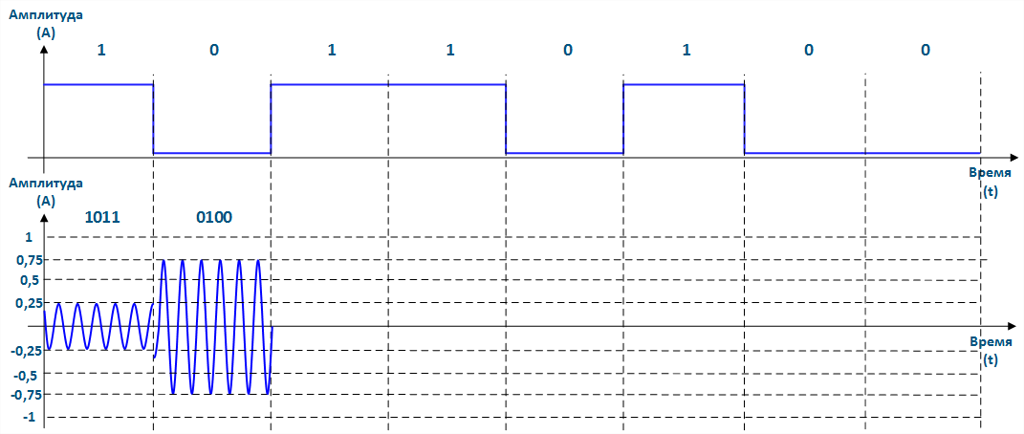
Рисунок 11 - Осциллограммы QAM-16
Мультиплексирование с ортогональным частотным разделением каналов (OFDM)
Одной из проблем при распространении сигнала, как было показано в уроке "Принципы распространения радиосигнала", является многолучёвость, последствием которой является межсимвольная интерференция (МСИ). Одним из методов борьбы с МСИ является использование OFDM, применение которого делит используемый частотный диапазон на множество поднесущих, на каждой из которых используется сниженная модуляция с большим защитным интервалом, сохраняя при этом общую скорость передачи. Кроме того, использование OFDM позволяет повысить устойчивость системы к частотно-избирательным замираниям, поскольку влияние будет оказано лишь на отдельные поднесущие, а не на весь спектр сигнала. Недостатком метода является чувствительность к эффекту Допплера.
Рассмотрим пример с использованием 8 OFDM-поднесущих, каждая из которых модулируется QAM-16. Пример проиллюстрирован на рисунке 12. Поскольку тип манипуляции на каждой поднесущей QAM-16, то одна символьная посылка соответствует передаче 4 бит информации. По этой причине информационный битовый поток необходимо разбить на блоки по 4 бита. Далее, каждому из четырёхбитных блоков ставится в соответствие фаза и амплитуда высокочастотного сигнала - символьная посылка. На следующем этапе символьный поток (не путать с битовым потоком исходных данных) распределяется в 8 параллельных каналов в соответствии с числом поднесущих.
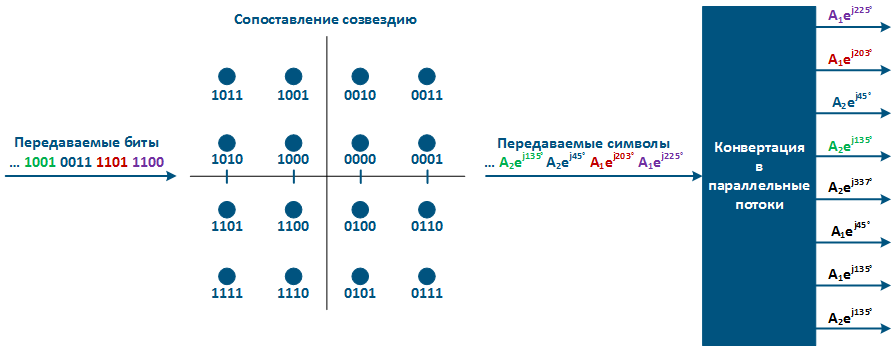
Рисунок 12 - Распределение потока информационных бит по восьми каналам с манипуляцией QAM-16 в каждом
Далее, каждый из потоков поступает в радиотракт, где каждый из них переносится на заданную частоту и передаётся в эфир:
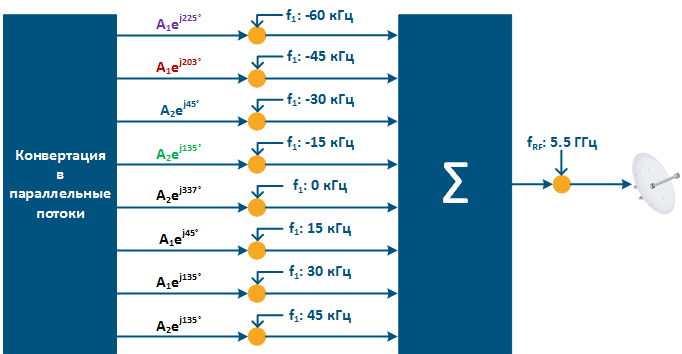
Рисунок 13 - Распределение сформированных потоков по поднесущим в радиотракте
На приёмной стороне проводятся преобразования в радиотракте, обратные рассмотренным, после чего оценивается фаза и амплитуда сигнала на каждой из поднесущих. После оценки параметров сигнала, он соотносится с разрешённым сигнальным созвездием - оранжевая точка на рисунке 14(а). Поскольку, в процессе распространения, параметры сигнала изменились, то он неточно соответствует разрешённому положению сигнального созвездия, однако, в данном случае, можно установить, что передана последовательность "0001", т.к. она ближайшая. Таким образом, в созвездии можно очертить область вокруг каждого из разрешённых сигналов, к которому будут сводиться принятые сигналы, параметры которых попадут в эту область. Например, можно использовать квадратные области, как на рисунке 14(б).
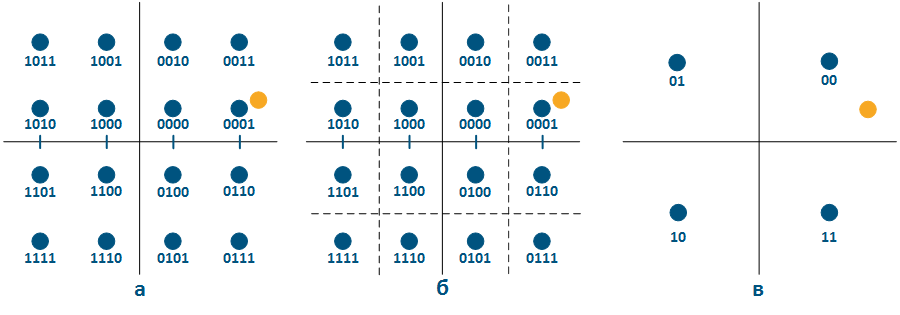
Рисунок 14 - Сопоставление принятого сигнала и сигнального созвездия на приёмной стороне при QAM-16 (а и б) и QAM-4 (в)
Однако, в случае, если при распространении сигнал сильно искажается и, на самом деле, была передана другая последовательность, например "0011", то возникает ошибка. В беспроводных системах связи, с помощью периодической рассылки служебных сообщений, происходит постоянный контроль за параметрами радиоканала и, в случае возникновения описанной ситуации, система может понизить манипуляцию, например до QAM-4. Это позволит снизить число ошибок при передаче ценой снижения скорости в канале. Сигнальное созвездие после смены манипуляции представлено на рисунке 14(в). При снижении манипуляции, увеличивается область вокруг каждого из разрешённых состояний, что непосредственно влияет на уровень ошибок при передаче.
Скорость передачи данных
Скорость передачи данных непосредственно связана с методом кодирования и используемого метода манипуляции. Рассмотрим пример, когда используется один частотный канал с манипуляцией QAM-64 5/6, т.е. одна символьная посылка соответствует шести битам данных. Кроме того исходная последовательность кодируется таким образом, что к каждым 5 битам исходной последовательности добавляется 1 избыточный бит. Пускай длительность одной символьной посылки 1 мкс, тогда:
